Figure 1 4 The surface defined by f (x, y)= radicalBig 1 − x 2 − y 2 1 3 1 Level curves Another way of visually representing functions of two variables is by using level curves Suppose f D −→ R is a function of two variables Then the set of points (x, y) in D satisfying the equation f (x, y)= k where k is some real constantOne way to collapse the graph of a scalarvalued function of two variables into a twodimensional plot is through level curves A level curve of a function f (x, y) is the curve of points (x, y) where f (x, y) is some constant value A level curve is simply a cross section of the graph of z = f (x, y) taken at a constant value, say z = cLevel Curves and Contour Maps The level curves of a function f(x;y) of two variables are the curves with equations f(x;y) = k, where kis a constant (in the range of f) A graph consisting of several level curves is called a contour map Level Surfaces The level surfaces of a function f(x;y;z) of three variables are the surfaces
Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id
Level curves of a function of two variables
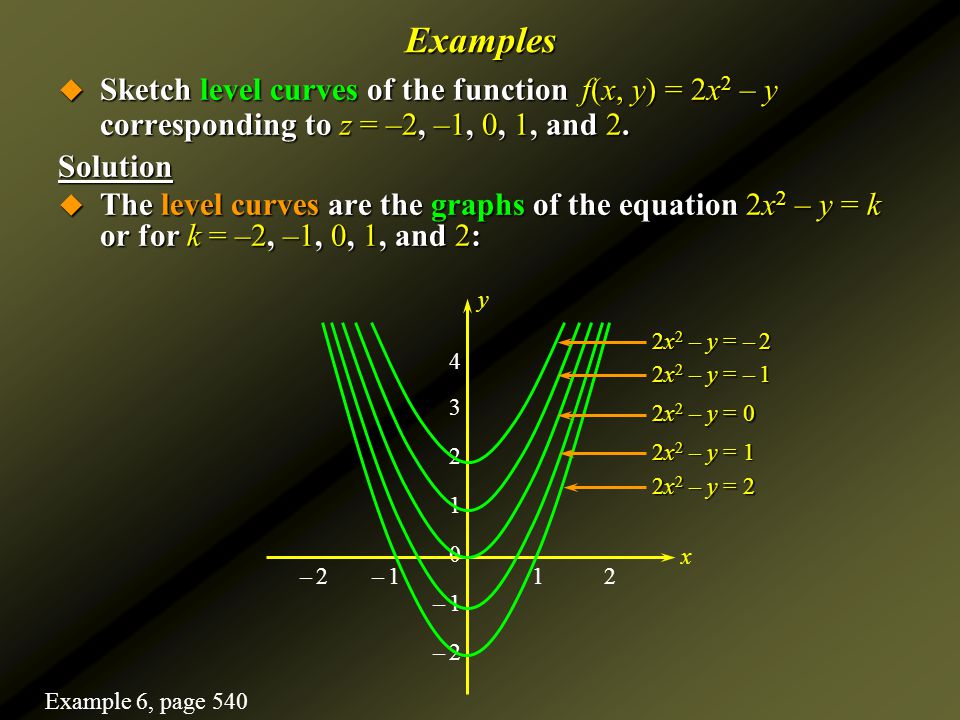
Level curves of a function of two variables-Definition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height kSay for example I give you a function of two variables z = f (x, y) = x 2 y 2 which represents a paraboloid If I want the level curves f (x, y) = c, then these now represent concentric circles in the x − y plane centered at the origin of radius c Now here's my question



Sin X Y Sin X 2 Y 2 Images To Visualizing Functions Of Two Variables Geogebra
Level Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, theOne primary difference, however, is that the graphs of functions of more than two variables cannot be visualized directly, since they have dimension greater than three However, we can still use slice curves, slice surfaces, contours, and level sets to examine these higherdimension functionsX y 143 Level Curves and Level Surfaces Look over book examples!!!
Functions of Several Variables (71) Part 2 1 Level Curves De nition 11 Level curves of a function of two variables The level curves of a function f of two variables are the curves with equations f(x;y) = k, where k is a constant in the range of f A level curve f(x;y) = k is the set of all points in the domain of f at which f takes on aThe remaining arguments are optional The next one specifies the particular MATLAB plotting function that will be used The defaults are 'plot' for functions of one variable or two component parametrized curves, 'plot3' for three dimensional parametrized curves, and 'surf' for functions of two variables or parametrized surfaces» Clip Level Curves and Contour Plots () From Lecture 8 of 1802 Multivariable Calculus, Fall 07 Flash and JavaScript are required for this feature
Be able to describe and sketch the domain of a function of two or more variables Know how to evaluate a function of two or more variables Be able to compute and sketch level curves & surfaces PRACTICE PROBLEMS 1 For each of the following functions, describe the domain in words Whenever possible, draw a sketch of the domain as well (a) fLevel curves allow to visualize functions of two variables f(x,y) Example For f(x,y) = x2− y2 the set x2− y2= 0 is the union of the lines x = y and x = −y The set x2− y2= 1 consists of two hyperbola with with their "noses" at the point (−1,0) and (1,0) The next topic that we should look at is that of level curves or contour curves The level curves of the function z = f (x,y) z = f (x, y) are two dimensional curves we get by setting z = k z = k, where k k is any number So the equations of the level curves are f (x,y) = k f (x, y) = k




1 Let The Function Of Two Variables Be Given As A Chegg Com



Http Www Math Harvard Edu Knill Teaching Summer18 Handouts Week2 Pdf
Given a function f(x, y) and a number c in the range of f, a level curve of a function of two variables for the value c is defined to be the set of points satisfying the equation f(x, y) = c Returning to the function g(x, y) = √9 − x2 − y2, we can determine the level curves of this function The range of g is the closed interval 0, 3This video is a gentle introduction to functions of several variables We motivate the topic and show how to sketch simple surfaces associated with functionA function of three variables is a hypersurface drawn in 4 dimensions There are a few techniques one can employ to try to "picture'' a graph of three variables One is an analogue of level curves level surfaces Given




Domain And Range Of A Function Of Two Variables Youtube




Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download
The curves we define when we fix one of the independent variables in our two variable function are called tracesTwo common ways of representing the graph of a function of two variables are the surface plot and the contour plot The first is simply a representation of the graph in threedimensional space The second, draws the level curves f ( x , y )= C for several values of C in the x , y plane The syntax of the command is the threevariable version of the syntax of the ContourPlot command to generate the level curves of a function of two variables ContourPlot3DFx, y, z, {x, xmin, xmax}, {y, ymin, ymax}, {z, zmin, zmax}




Level Sets Math Insight




Calculus Iii Functions Of Several Variables
(a) The level curves of a function of two variables are specified as f(x,y) =const Express the derivative of this function at any point (x,y) in terms of the partial derivatives of f(x,y) Draw some level curves of the real and imaginary parts of the function w = z'in the (x,y) planeMy Partial Derivatives course https//wwwkristakingmathcom/partialderivativescourseIn this video we're talking about how to sketch the level curves ofMATH 1 Multivariable Calculus at Queens College, Spring 21




Level Sets Math Insight



8 Calculus Of Several Variables Functions Of Several Variables Ppt Download
Calculus 3 Lecture 131 Intro to Multivariable Functions (Domain, Sketching, Level Curves) Working with Multivariable Functions with an emphasis on findiLevel curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant For example the curve at height zA level curve can be drawn for function of two variable ,for function of three variable we have level surface A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of f



Draw Level Curves For Functions Of Two Variables In C C Helper




Document
When we talk about the graph of a function with two variables defined on a subset D of the xyplane, we mean zfxy xy D= (, ) ,( )∈ If c is a value in the range of f then we can sketch the curve f(x,y) = cThis is called a level curve A collection of level curves can give a good representation of the 3d graphLevel sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour ofLevel Curves and Surfaces Example 2 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level set



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf




Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram
f (x,y) = 1 x √y 4 −√x1 f (x, y) = 1 x y 4 − x 1 Solution For problems 5 – 7 identify and sketch the level curves (or contours) for the given function 2x−3y z2 =1 2 x − 3 y z 2 = 1 Solution 4z2y2−x =0 4 z 2 y 2 − x = 0 Solution A function of one variable is a curve drawn in 2 dimensions;While technology is readily available to help us graph functions of two variables, there is still a paperandpencil approach that is useful to understand and master as it, combined with highquality graphics, gives one great insight into the behavior of a function This technique is known as sketching level curves



Functions Of Two Variables Lessons Blendspace



7 Points Below Are Four Contour Diagrams Each Giving Level Curves Of A Function Of Two Variables Click On An Image To Enlarge It A B C D Course Hero
The graph of a function of two variables is a surface in and can be studied using level curves and vertical traces A set of level curves is called a contour mapExample 72 Suppose we want to describe the elevation above see level of each point on the surface of a mountain For simplicity, suppose that the mountain just looks like a cone, with the base at sea level The altitude can be represented by the function \\begin{eqnarray*} fD & \longrightarrow & {\mathbb R} \\ z & = & f(x,y), \end{eqnarray*}\ associating to each point in theFor a function of three variables, one technique we can use is to graph the level surfaces, our threedimensional analogs of level curves in two dimensions Given , the level surface at is the surface in space formed by all points where



Announcements Topics To Do Ppt Download




14 Partial Derivatives Partial Derivatives So Far We
A function of two variables is a surface drawn in 3 dimensions;Differentiation of Functions of Several Variables Section 1 Functions of Several Variables Select Section 41 Functions of Several Variables 42 Limits and Continuity 43 Partial Derivatives 44 Tangent Planes and Linear Approximations 45 The Chain Rule 46 Directional Derivatives and the Gradient 47 Maxima/Minima Problems 48Functions of 2 Variables, Graphs, Level Curves Functions of 3 Variables, Level Surfaces Calculus of Multivariable Functions, Limits, TwoPath Test Week 5 Sec Partial First and Higher Order Derivatives, Clairaut Theorem, Differentiability Chain Rule, Implicit Differentiation Gradient, Directional Derivative Week 6



Mysite Science Uottawa Ca ionne Teaching Help Centre Level Curve Pdf




Multivariable Functions And Their Level Curves Dave4math
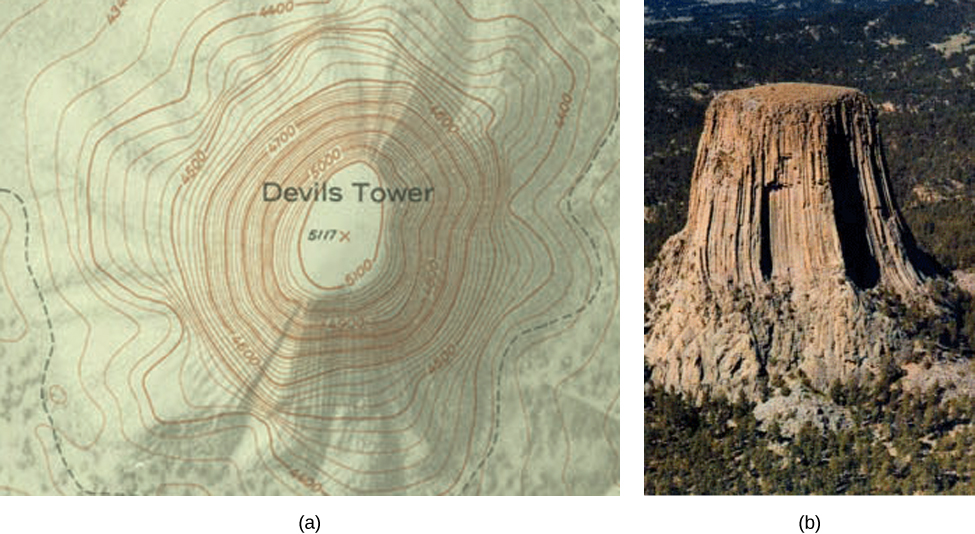
So level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplane And if we're being careful and if we take the convention that our level curves are evenly spaced in the zplane, then these are going to get closer and closer together, and we'll see in a minute where that's coming fromTranscribed image text CURRENT OBJECTIVE Find the level curves of a function of two variables Question Choose the most specific description for the level curve of the function g(1,y) = zhy corresponding to c= 2 Select the correct answer below a line passing through the origin, excluding the origin a line passing through the origin O parabola ellipseA level curve of a function of two variables f (x, y) f (x, y) is completely analogous to a contour line on a topographical map Figure 47 (a) A topographical map of Devil's Tower, Wyoming Lines that are close together indicate very steep terrain (b) A perspective photo of Devil's Tower shows just how steep its sides are
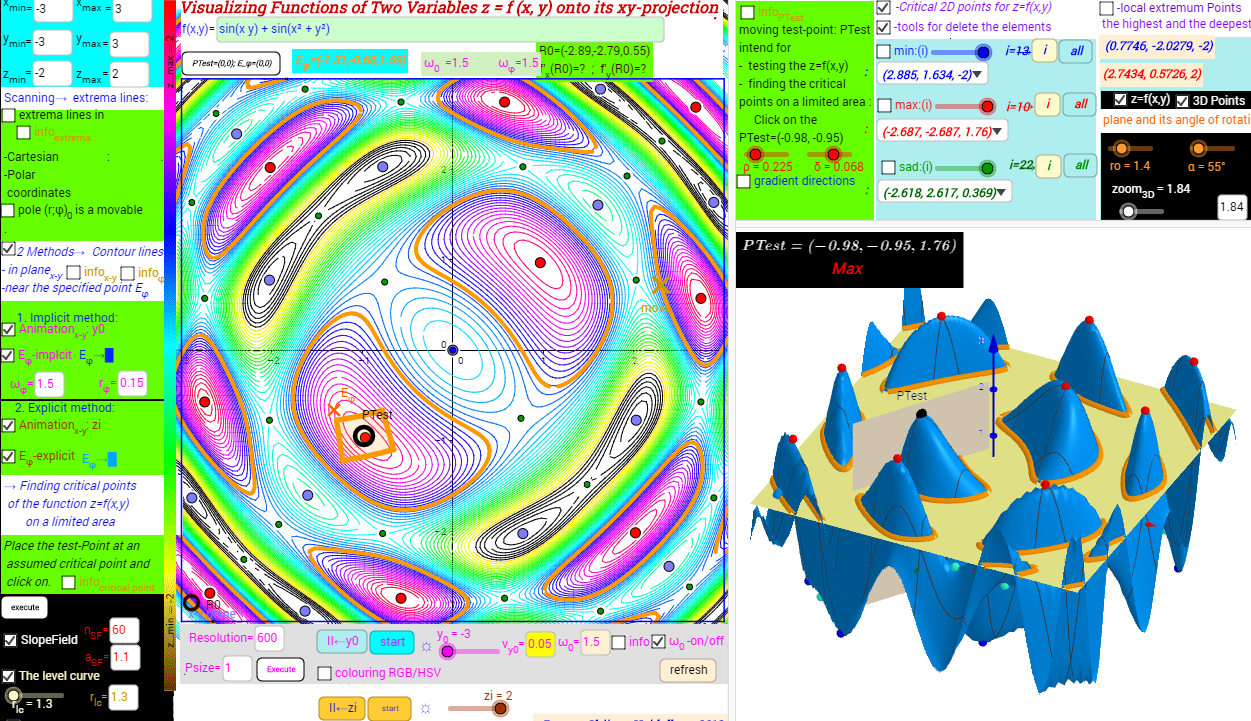



Sin X Y Sin X 2 Y 2 Images To Visualizing Functions Of Two Variables Geogebra




Lecture Notes Chapter 1 1 Part2 Contourlines Level Curves And 3d Graphs Contour Line Function Mathematics
Level Curves and Surfaces The graph of a function of two variables is a surface in space Pieces of graphs can be plotted with Maple using the command plot3dFor example, to plot the portion of the graph of the function f(x,y)=x 2 y 2 corresponding to x between 2 and 2 and y between 2 and 2, type > with (plots);141 Functions of Several Variables In singlevariable calculus we were concerned with functions that map the real numbers R to R, sometimes called "real functions of one variable'', meaning the "input'' is a single real number and the "output'' is likewise a single real number In the last chapter we considered functions taking a real numberC Graph the level curve AHe, iL=3, and describe the relationship between e and i in this case T 37 Electric potential function The electric potential function for two positive charges, one at H0, 1L with twice the strength as the charge at H0, 1L, is given by fHx, yL= 2 x2 Hy1L2 1 x2 Hy 1L2 a Graph the electric potential using the window @5, 5Dµ@5, 5Dµ@0, 10 D



1




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
The graph itself is drawn in an ( x, y, z) coordinate system Remark 2 Level curves of the same function with different values cannot intersect Remark 3 Level curves of utility functions are called indifference curves3 Functions of Two Variables The temperature T at a point on the surface of the earth at any given time depends on the longitude x and latitude y of the point We can think of T as being a function of the two variables x and y, or as a function of the pair (x, y)We indicate this functional dependence by writing T = f (x, y)The volume V of a circular cylinder depends on its radius rOf such functions We study functions of two variables in Sections 141 through 146 We discuss vertical cross sections of graphs in Section 141, horizontal cross sections and level curves in Section 142, partial derivatives in Section 143, Chain Rules in Section 144, directional derivatives and gradient vectors in




Introduction To Functions Of Several Variables



The Gradient And Directional Derivative
Remark 1 Level curves of a function of two variables can be drawn in an ( x, y) coordinate system;The level curves of a function f of two variables are the curves with equations f(x,y) = k lying in the domain of f, where k is a constant in the range of f The level curves are just the horizontal traces of the graph of f Example The function z = f(x,y) = Determine the directional derivative in a given direction for a function of two variables Determine the gradient vector of a given realvalued function Explain the significance of the gradient vector with regard to direction of change along a surface Use the gradient to find the tangent to a level curve of a given function




Level Set Examples Math Insight



Www Math Uci Edu Remote Teaching Lecture Notes Of Hamed Math 2d lecture notes Lecture note 14 1 Pdf




Level Curves Calculus




Functions Of Two And Three Variables Level Curves Contours Level Surfaces Youtube




Calculus Iii Functions Of Several Variables




Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id
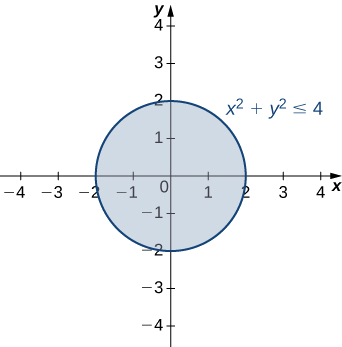



13 1 Functions Of Several Variables Mathematics Libretexts



2



12 5 Functions Of Three Variables




Functions Of Two Variables Graph Of A Function




13 1 Functions Of Several Variables Mathematics Libretexts



12 1 Introduction To Multivariable Functions Mathematics Libretexts
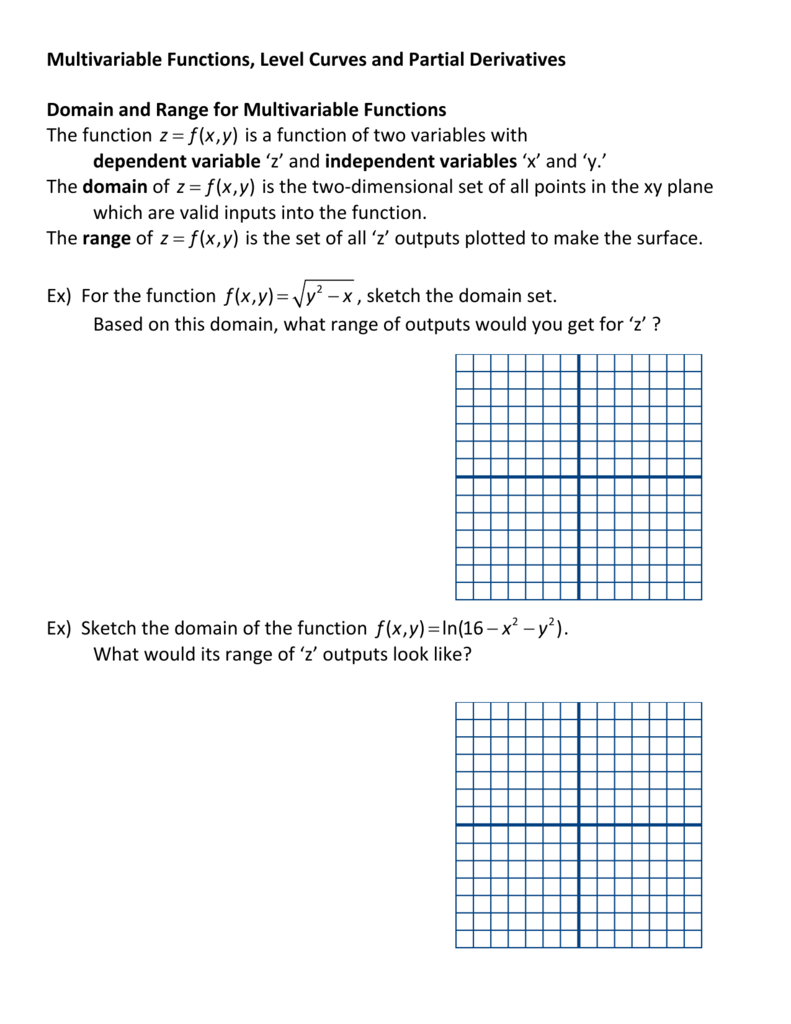



Multivariable Functions Level Curves And Partial Derivatives




Level Sets Math Insight




Sin X Y Sin X 2 Y 2 Images To Visualizing Functions Of Two Variables Geogebra
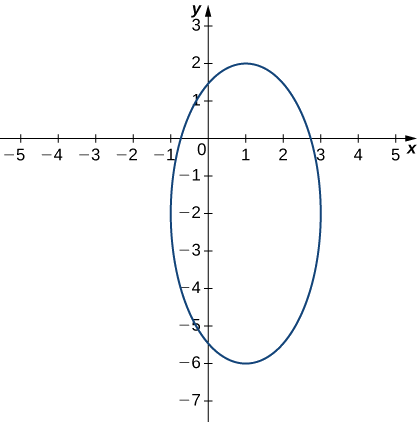



13 1 Functions Of Several Variables Mathematics Libretexts




How Do You Sketch Level Curves Of Multivariable Functions Youtube




Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id




Level Curves Of Functions Of Two Variables Youtube




In Calculus I And Ii We Worked With Functions Chegg Com




Level Curves Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Level Curves




Level Set Wikipedia
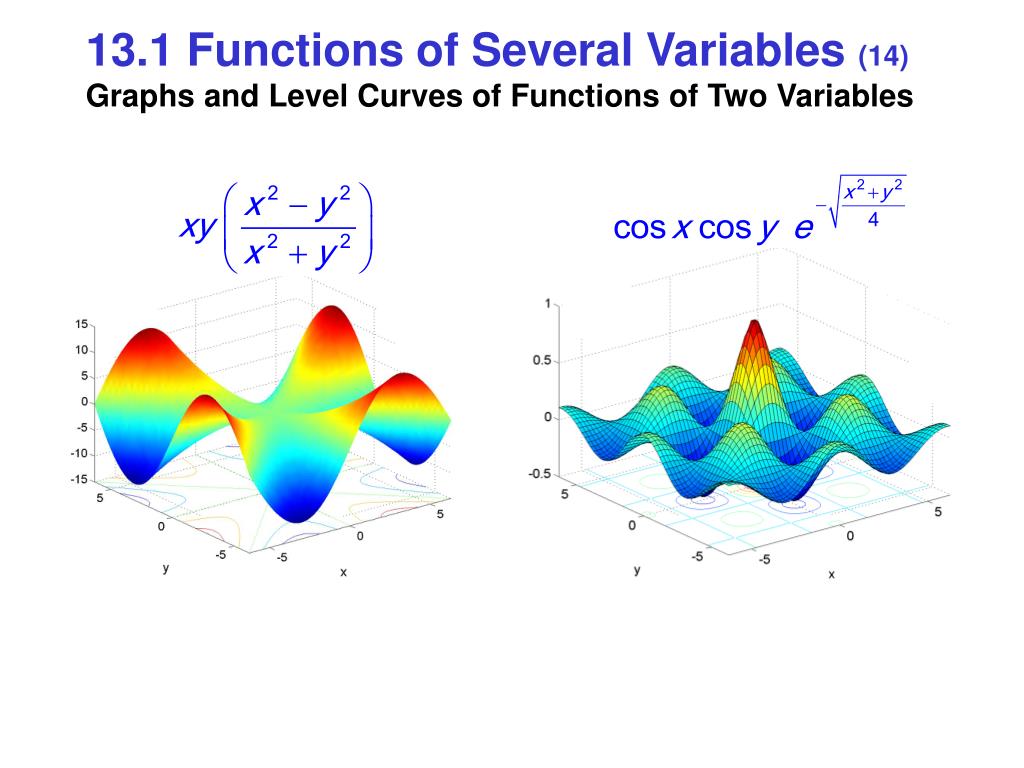



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id
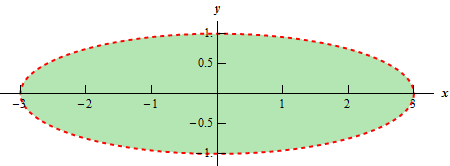



Calculus Iii Functions Of Several Variables
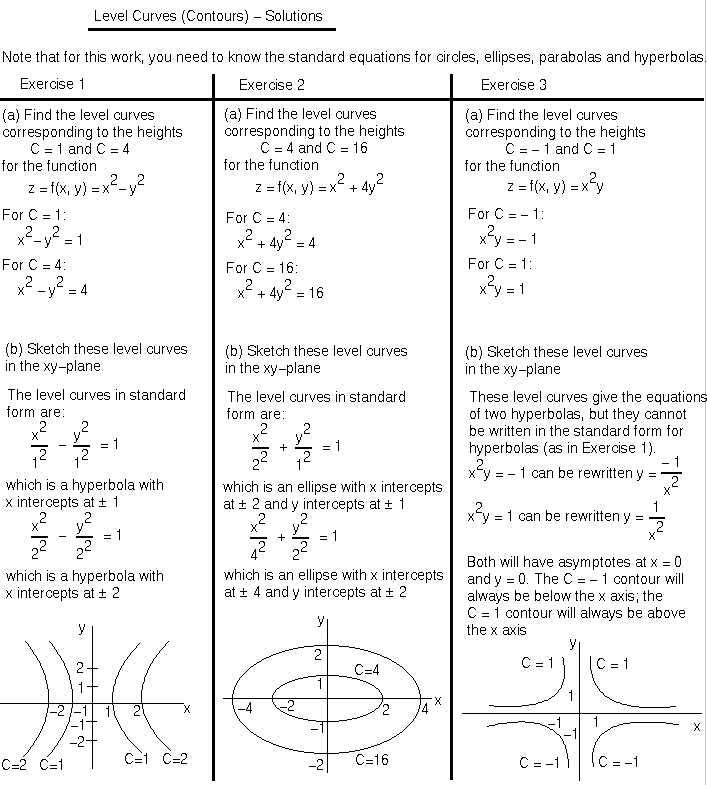



Functions Of Two Variables Math100 Revision Exercises Resources Mathematics And Statistics University Of Canterbury New Zealand
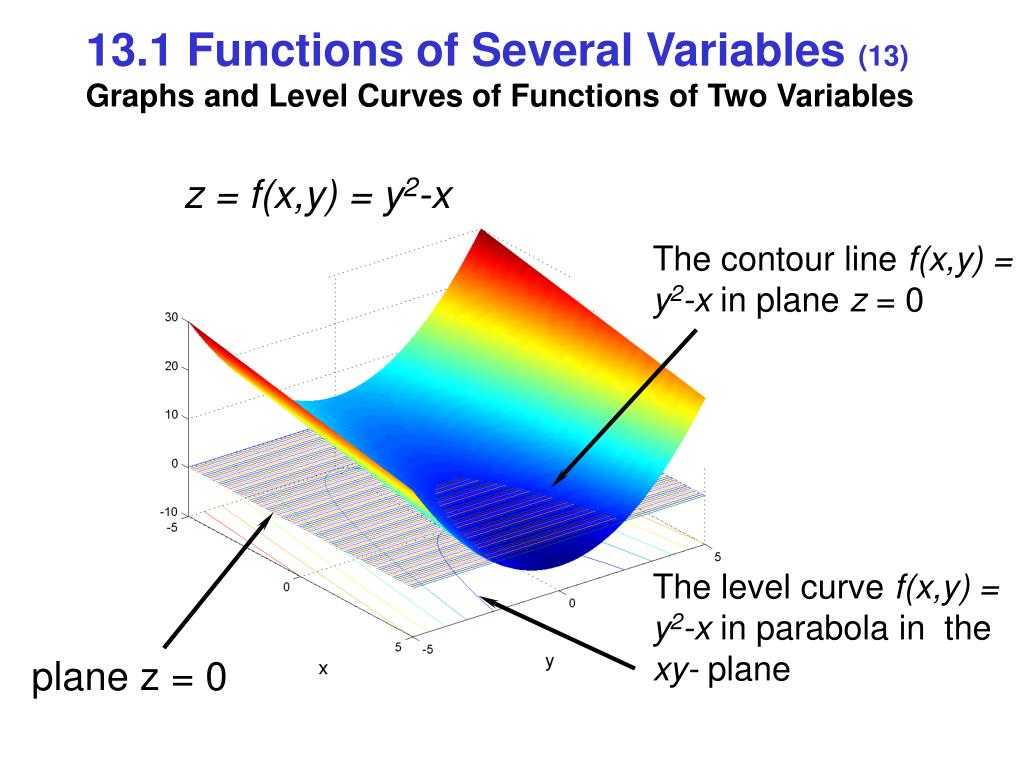



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id




Presentation On Introduction To Several Variables And Partial Derivat




Sketch Saddle Point Of A Function Of Two Variables F X Y 4 X 3 Y 3 3xy Stewart P930 Question 14 7 3 Mathematics Stack Exchange
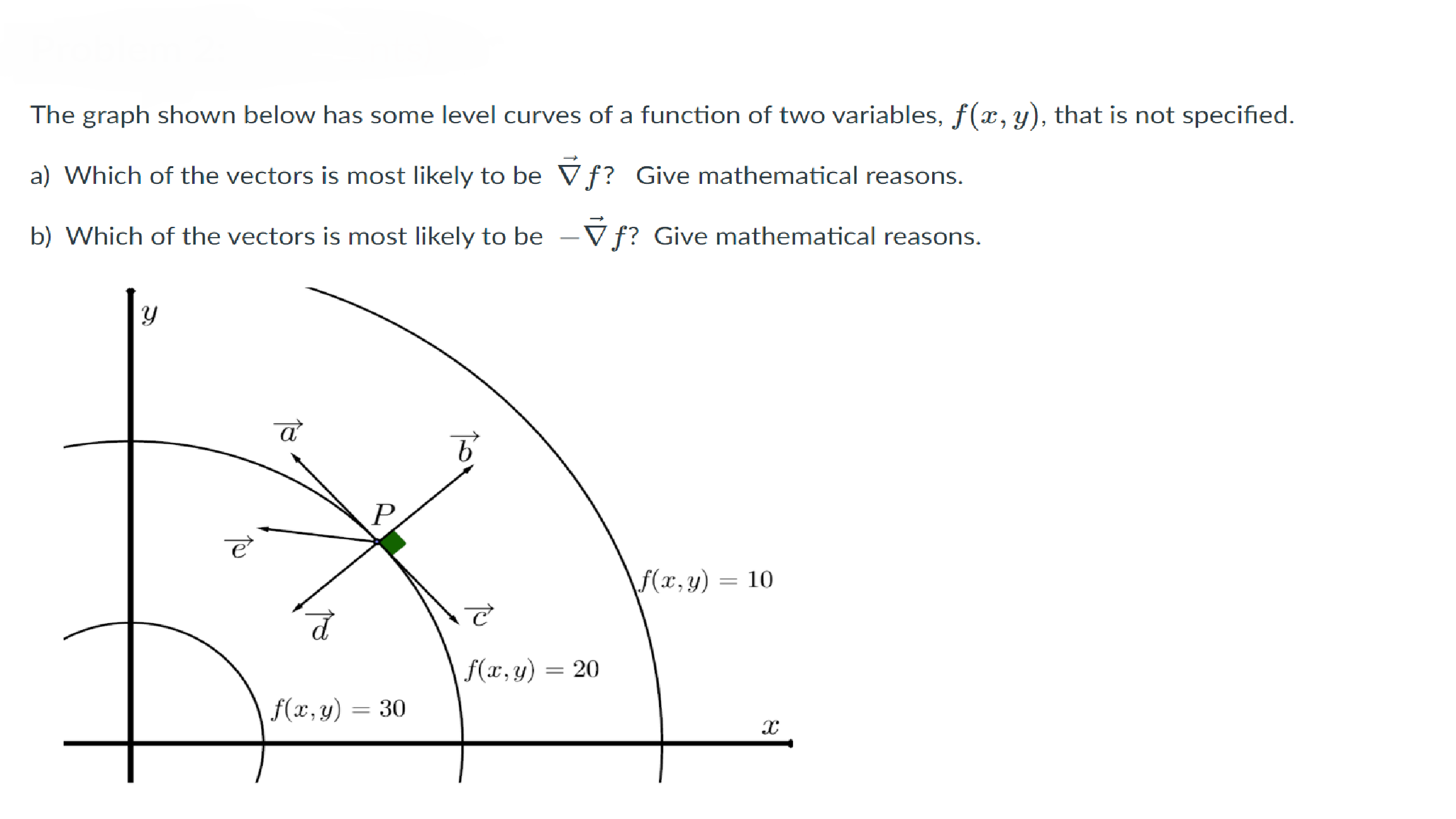



The Graph Shown Below Has Some Level Curves Of A Chegg Com
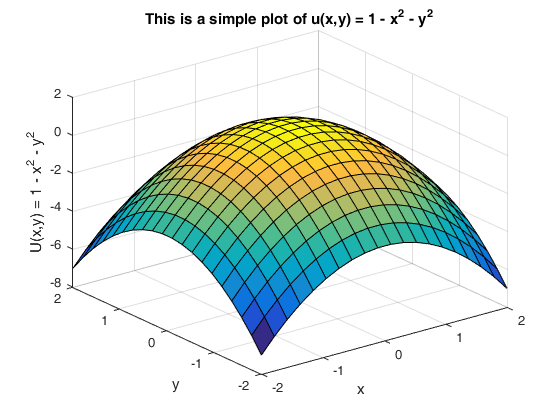



Howtoplotfunctiontwovariables




Level Set Examples Math Insight




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Lecture 4 Graph Level Curves Contour Lines Of Functions Of Two Variables Youtube
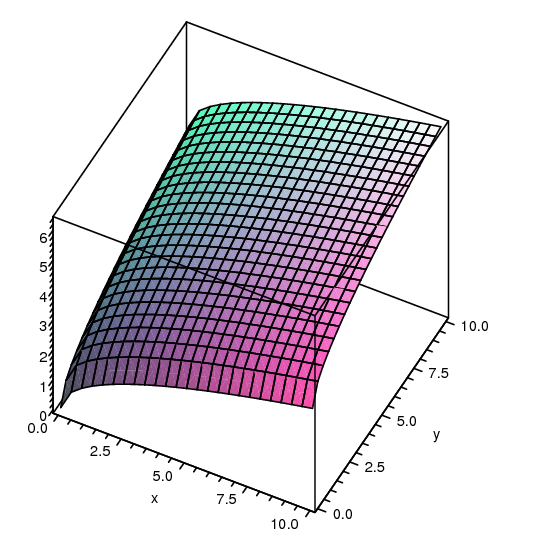



16 1 Functions Of Several Variables
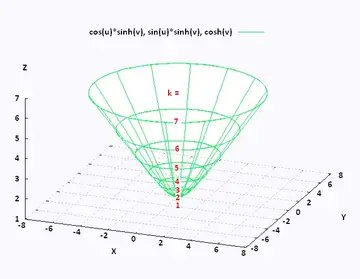



Mathematics Calculus Iii



Q Tbn And9gctwew2zrp6pwdmavaatloklnzlyvukd 496gz2fdomg9pxd4akz Usqp Cau
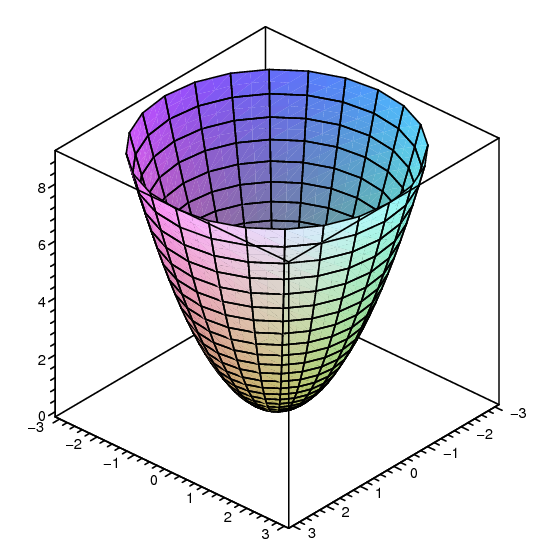



16 1 Functions Of Several Variables




Level Set Wikipedia



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf




Level Curves



Sites Fas Harvard Edu Maths21a Handouts Week2 Pdf
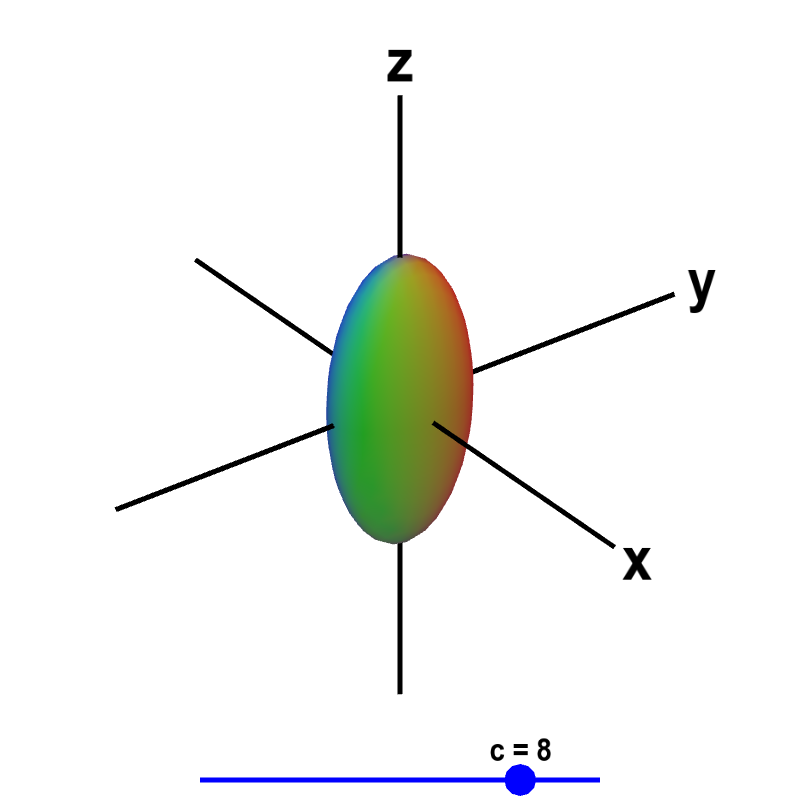



Level Sets Math Insight
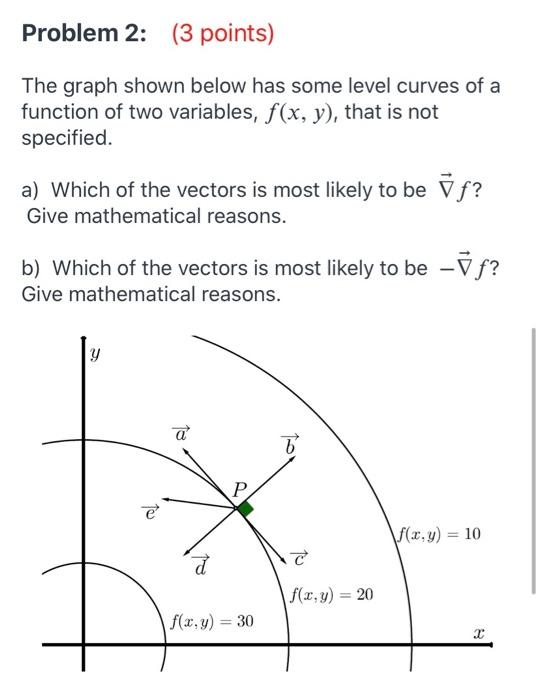



Problem 2 3 Points The Graph Shown Below Has Some Chegg Com




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Calculus Iii Functions Of Several Variables



Functions Of Several Variables




13 1 Functions Of Several Variables Mathematics Libretexts




Calculus Iii Functions Of Several Variables



Http Math Oregonstate Edu Garity 254h Winter13 Notes 10 Graphs Levelcurves Pdf




16 1 Functions Of Several Variables




Level Curves



Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download




How To Draw A Contour Map Calculus Maping Resources




28 36 38 40 41 15 1 Graphs And Level Curves 927 A Figure 15 18 Section 15 1 Homeworklib



1




Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download




1 Objective Functions In Two Variables Partial Differentiation




14 Partial Derivatives Copyright Cengage Learning All Rights



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework13 1 Ans Pdf



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf
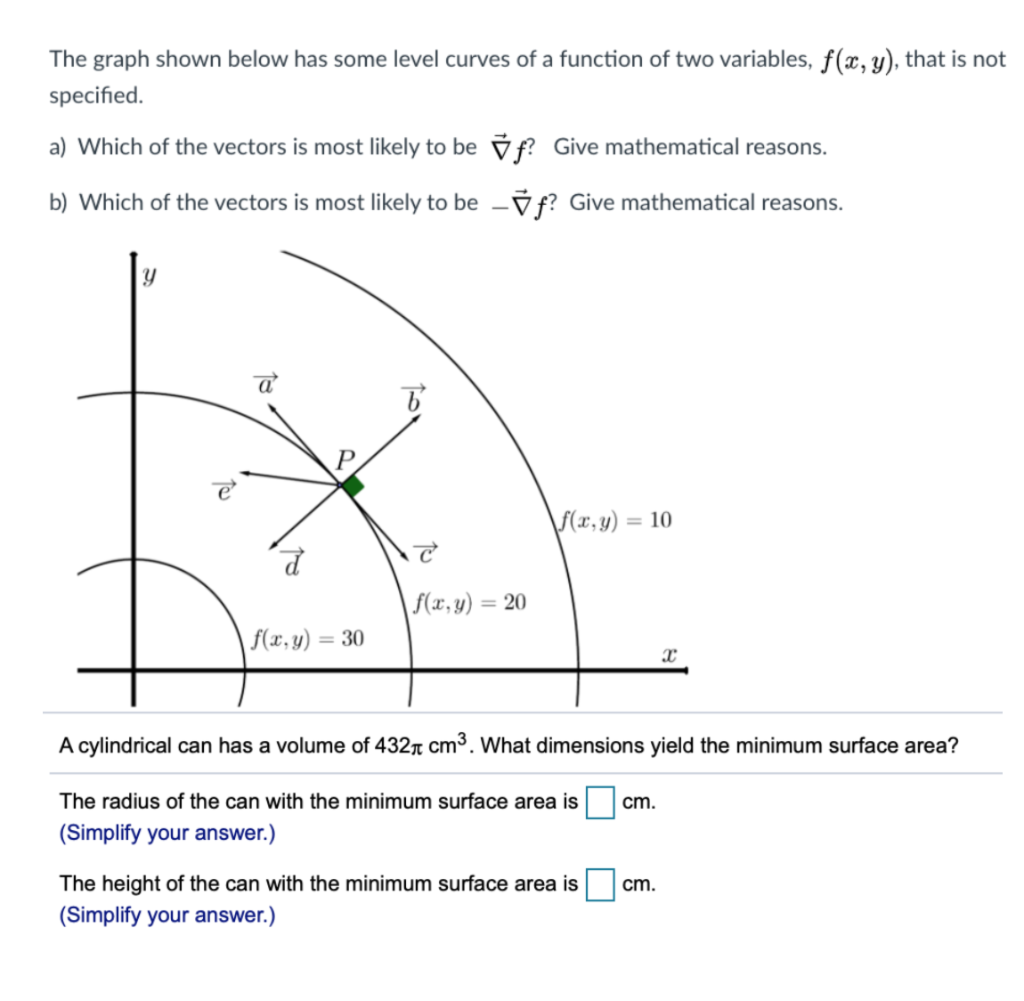



Solved The Graph Shown Below Has Some Level Curves Of A F Chegg Com



Http Diposit Ub Edu Dspace Bitstream 2445 1 Student E2 80 99s autonomous learning and tools for teachers by means of the use of geogebra 28 C3 81lvarez et al 18 29 Pdf




Level Curves And Implicit Differentiation Studocu




Level Curves



Calculus Iii Functions Of Several Variables




8 Calculus Of Several Variables U Functions Of
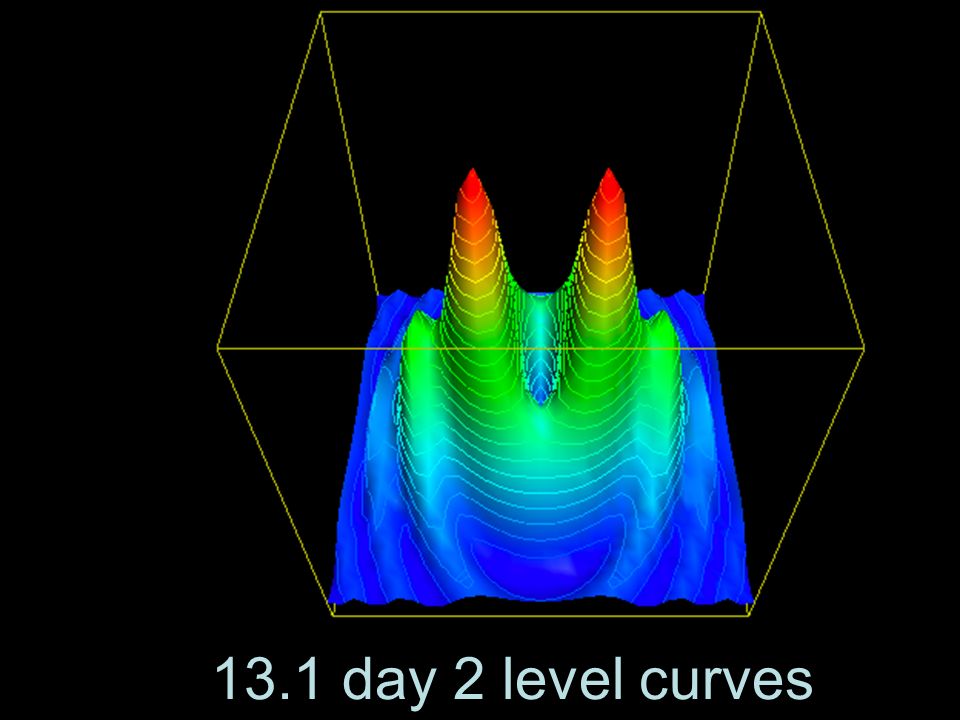



13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned



1




Level Set Wikipedia
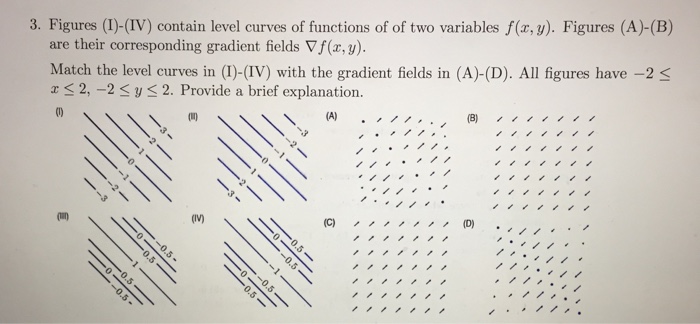



Figures I Iv Contain Level Curves Of Functions Of Chegg Com




Introduction To Functions Of Several Variables Ppt Download



Labware Ma35 Multivariable Calculus Two Variable Calculus
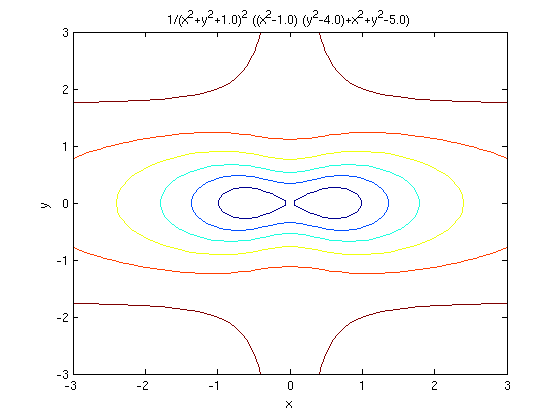



Visualizing Functions Of Several Variables And Surfaces
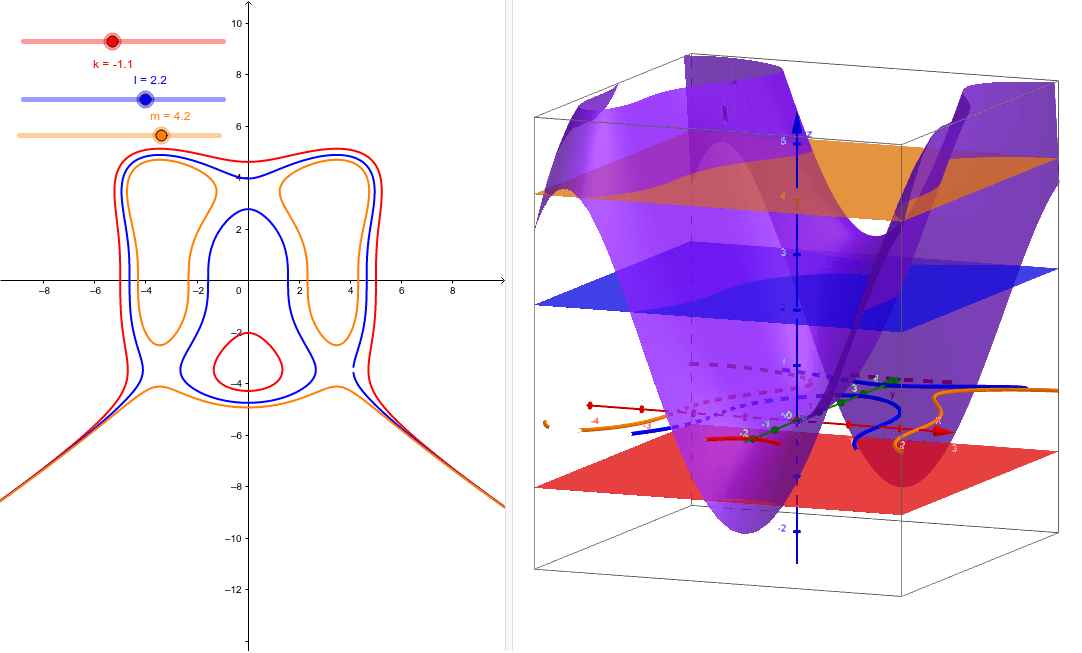



Function Of Several Variables Several Level Curves Geogebra



Level Curves Functions Of Several Variables By Openstax Page 3 12 Jobilize




Ppt Chapter 14 Partial Derivatives Powerpoint Presentation Free Download Id




3 Points Writing Prompt 1 Typed 100 0 Words In Chegg Com




11 Level Curves And Contour Lines Of Functions Of Two Variables Youtube



Calculus Iii Functions Of Several Variables



0 件のコメント:
コメントを投稿